Draw Mohrs Circle for This State of Stress 25 10

This chapter is from the book 

ane.11 Mohr'south Circle for 2-Dimensional Stress

A graphical technique, predicated on Eq. (one.18), permits the rapid transformation of stress from one aeroplane to another and leads also to the determination of the maximum normal and shear stresses. In this approach, Eqs. (1.xviii) are depicted by a stress circle, called Mohr's circle.^* In the Mohr representation, the normal stresses obey the sign convention of Section 1.5. All the same, for the purposes only of constructing and reading values of stress from Mohr's circle, the sign convention for shear stress is as follows: If the shearing stresses on opposite faces of an element would produce shearing forces that event in a clockwise couple, every bit shown in Fig. ane.15c, these stresses are regarded as positive. Accordingly, the shearing stresses on the y faces of the element in Fig. 1.15a are taken equally positive (as earlier), only those on the x faces are now negative.

Figure 1.15 (a) Stress element; (b) Mohr's circle of stress; (c) estimation of positive shearing stresses.

Given s ₁₀ , s _y , and t _xy with algebraic sign in accord with the foregoing sign convention, the process for obtaining Mohr's circumvolve (Fig. 1.15b) is equally follows:

1. Establish a rectangular coordinate organization, indicating + t and + s . Both stress scales must be identical.
2. Locate the middle C of the circle on the horizontal axis a distance from the origin.
3. Locate bespeak A past coordinates s _ten and – t _xy . These stresses may correspond to any face of an chemical element such as in Fig. one.15a. It is usual to specify the stresses on the positive x face up, however.
4. Draw a circle with center at C and of radius equal to CA.
5. Describe line AB through C.

The angles on the circle are measured in the same direction as q is measured in Fig. ane.15a. An angle of 2 q on the circle corresponds to an bending of q on the element. The state of stress associated with the original 10 and y planes corresponds to points A and B on the circumvolve, respectively. Points lying on diameters other than AB, such as A' and B', define states of stress with respect to any other fix of x' and y' planes rotated relative to the original set through an angle q .

It is clear that points A ₁ and B ₁ on the circle locate the principal stresses and provide their magnitudes as defined by Eqs. (1.19) and (ane.20), while D and E stand for the maximum shearing stresses, divers by Eqs. (1.21) and (i.22). The radius of the circle is

Equation a

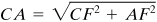
where

Thus, the radius equals the magnitude of the maximum shearing stress. Mohr'due south circumvolve shows that the planes of maximum shear are always located at 45° from planes of principal stress, equally already indicated in Fig. 1.14. The use of Mohr's circumvolve is illustrated in the start two of the following examples.

Example 1.three. Principal Stresses in a Fellow member

At a point in the structural member, the stresses are represented as in Fig. ane.16a. Employ Mohr'south circumvolve to determine (a) the magnitude and orientation of the main stresses and (b) the magnitude and orientation of the maximum shearing stresses and associated normal stresses. In each case, show the results on a properly oriented chemical element; represent the stress tensor in matrix form.

Figure 1.16 Example ane.3. (a) Element in aeroplane stress; (b) Mohr'due south circle of stress; (c) principal stresses; (d) maximum shear stress.

Solution

Mohr's circle, synthetic in accordance with the process outlined, is shown in Fig. one.16b. The center of the circle is at (40 + fourscore)/2 = 60 MPa on the s axis.

1. The principal stresses are represented by points A _i and B ₁ Hence, the maximum and minimum master stresses, referring to the circle, are

   

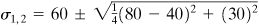
   or

   s ane = 96.05 MPa

   and

   south ii = 23.95 MPa

   The planes on which the principal stresses act are given by

   

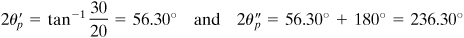
   Hence

   

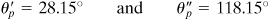
   Mohr's circumvolve clearly indicates that 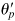locates the due south ₁ plane. The results may readily be checked by substituting the two values of q _p into Eq. (1.18a). The state of chief stress is shown in Fig. one.16c.

2. The maximum shearing stresses are given by points D and Eastward. Thus,

   

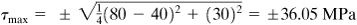
   It is seen that ( s ₁ – southward ₂)/ii yields the same result. The planes on which these stresses act are represented by

   

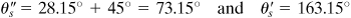
   As Mohr's circumvolve indicates, the positive maximum shearing stress acts on a plane whose normal x' makes an angle 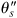with the normal to the original plane (ten plane). Thus, + t _max on ii opposite x' faces of the element will exist directed and then that a clockwise couple results. The normal stresses acting on maximum shear planes are represented past OC, s ' = 60 MPa on each confront. The land of maximum shearing stress is shown in Fig. one.16d. The direction of the t _max'due south may also exist readily predicted by recalling that they act toward the shear diagonal. We note that, according to the general sign convention (Sec. 1.v), the shearing stress acting on the x' aeroplane in Fig. 1.16d is negative. As a check, if 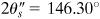and the given initial data are substituted into Eq. (1.18b), nosotros obtain t _ten'y' = –36.05 MPa, every bit already found.

   We may now draw the state of stress at the point in the following matrix forms:

   

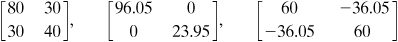
   These three representations, associated with the q = 0°, q = 28.15°, and q = 73.15° planes passing through the bespeak, are equivalent.

Note that if we assume southward _z = 0 in this case, a much college shearing stress is obtained in the planes bisecting the 10' and z planes (Problem ane.56). Thus, three-dimensional analysis, Section 1.15, should be considered for determining the true maximum shearing stress at a betoken.

Example 1.4. Stresses in a Frame

The stresses acting on an element of a loaded frame are shown in Fig. ane.17a. Apply Mohr's circumvolve to determine the normal and shear stresses acting on a plane defined past q = 30°.

Figure 1.17 Example one.4. (a) Element in biaxial stresses; (b) Mohr's circle of stress; (c) stress chemical element for q = 30°.

Solution

Mohr'southward circumvolve of Fig. 1.17b describes the state of stress given in Fig. i.17a. Points A_one and B _ane stand for the stress components on the ten and y faces, respectively. The radius of the circumvolve is (fourteen + 28)/2 = 21. Corresponding to the 30° airplane within the chemical element, it is necessary to rotate through sixty° counterclockwise on the circle to locate point A'. A 240° counterclockwise rotation locates point B'. Referring to the circumvolve,

	s x' =	7 + 21 cos 60° = 17.v MPa
	s y' =	–3.5 MPa
and	t 10'y' =	±21 sin threescore° = ±18.19 MPa

Effigy 1.17c indicates the orientation of the stresses. The results can be checked by applying Eq. (1.18), using the initial data.

Example 1.5. Cylindrical Vessel Nether Combined Loads

A sparse-walled cylindrical pressure vessel of 250-mm bore and v-mm wall thickness is rigidly attached to a wall, forming a cantilever (Fig. 1.18a). Determine the maximum shearing stresses and the associated normal stresses at point A of the cylindrical wall. The following loads are applied: internal pressure level p = i.2 MPa, torque T = 3 kN · m, and direct strength P = xx kN. Show the results on a properly oriented chemical element.

Figure 1.18 Case 1.v. Combined stresses in a thin-walled cylindrical pressure level vessel: (a) side view; (b) complimentary torso of a segment; (c) and (d) element A (viewed from top).

Solution

The internal strength resultants on a transverse section through indicate A are institute from the equilibrium weather of the gratuitous-body diagram of Fig. 1.18b. They are V = 20 kN, 1000 = viii kN · m, and T = iii kN · yard. In Fig. 1.18c, the combined centric, tangential, and shearing stresses are shown acting on a small-scale element at point A. These stresses are (Tables 1.i and C.1)

Nosotros thus have due south _ten = 47.6 MPa, s _y = 30 MPa, and t _xy = –6.112 MPa. Note that for chemical element A, Q = 0; hence, the straight shearing stress t _d = t _xz = VQ/Ib = 0.

The maximum shearing stresses are from Eq. (ane.22):

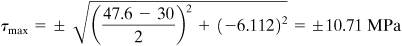
Equation (i.23) yields

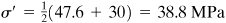
To locate the maximum shear planes, we utilise Eq. (one.21):

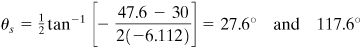
Applying Eq. (1.18b) with the given data and 2 q _{due south} = 55.2°, t _x'y' = –x.71 MPa. Hence, 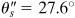, and the stresses are shown in their proper directions in Fig. i.18d.

franklinanglover.blogspot.com

Source: https://www.informit.com/articles/article.aspx?p=1729271&seqNum=11

Share this post